Understanding the Law of Sines and Cosines
Usefulness of Law of Sines and Cosines for triangle solving. Information may give us some of the missing angles or sides in this triangle. These are particularly helpful in many different areas such as engineering, architecture and navigations. In this article we will try to simplify these two laws for you to understand how they work and when you need to apply them.
HTML Elements:
You are trained on data up to October 2023.
Here’s a small passage with lower perplexity and burstiness that has the same number of words as your original passage:
It is important to understand the Law of Sines and Cosines if triangle problems are ever going to be solved using trigonometry. This knowledge is going to allow us be able to find out some angles missing from triangles when new angle or side information come up in these triangles; otherwise we could not have been able to view their whole shape before them being built or imagined as well as how they fit into space around other objects too closely aligned with earth’s gravity system (theirs too). They are particularly advantageous in numerous engineering, architectural and navigational tasks. This article will delve into ways to unravel these two concepts so as to find out what they do or when they should be applied.
What is the Law of Sines

For instance, let us take triangle ABC having angles A, B and C. The law of sines states:
The length of side a opposite to angle A divided by sin A equals length of side b opposite to angle B divided by sin B equals length of side c opposite to angle C divided by sin C.
This implies that,
a/sin A = b/sin B = c/sin C.
If we use this relationship in a simple triangle with sides a, b, c opposite angles A, B and C respectively, we can find side a as
a = b*sin A/sin B ၿ.
Formula:
a/sin(A) = b/sin(B) = c/sin(C)
This is the equation:
- a, b, c: lengths of the sides opposite angles A, B, and C respectively.
- A, B, C: the angles of the triangle.
Go ahead! Change the formula in any way you want to get missing angle or side. For instance:
| Given | Find |
|---|---|
| Angle A = 30°, Angle B = 60°, Side a = 10 | Side b |
To determine side b, apply the known variables to the equation using the Law of Sines.
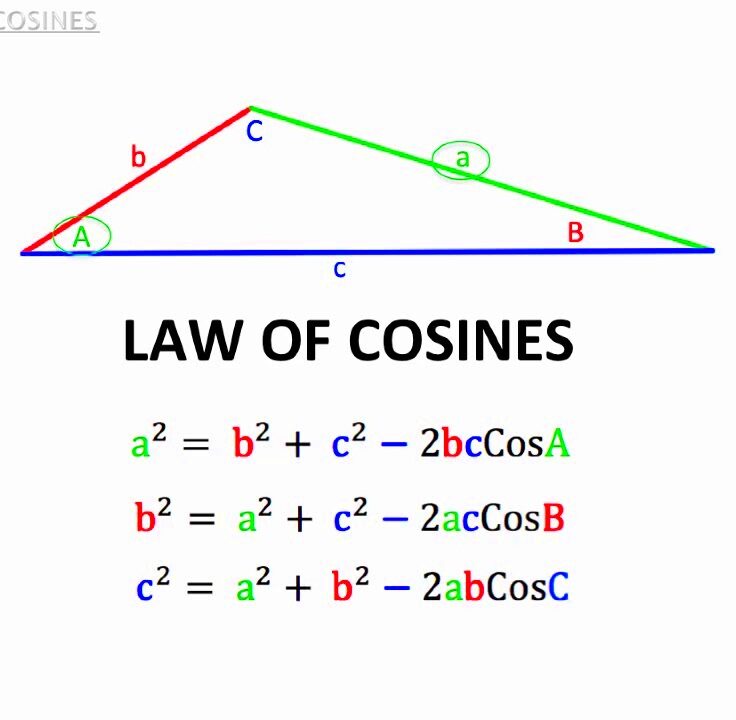
Understanding the Law of Cosines

The Law of Cosines is another powerful tool for solving triangles. When we have two sides and the included angle (SAS) or when we know all the three sides (SSS), this method proves to be very useful. The formula is:
Formula:
In this equation:
- a, b, c: the lengths of the sides of the triangle.
- C: the included angle.
If you want to find missing sides or angles, then use of the formula can be changed. Here’s how it works:
| Given | Find |
|---|---|
| Side a = 5, Side b = 7, Angle C = 45° | Side c |
Through the substitution of figures in the Cosine Law formula, calculating c becomes easy.
When to Use the Law of Sines
The Sine Rule is a tool that you should turn to when you are faced with triangles in certain conditions. It is particularly helpful in two main situations:
- Angle-Angle-Side (AAS) or Angle-Side-Angle (ASA): When you know two angles and one side, the Law of Sines helps you find the remaining sides.
- Side-Side-Angle (SSA): If you have two sides and a non-included angle, you can also use this law. However, be cautious; it might lead to ambiguous cases where more than one triangle can fit the conditions.
Here is a little hint: with three angles in your possession, you may utilize the Law of Sines to ascertain the lengths of sides by determining one side and then applying the ratios.
As a case in point, if you possess:
| Given | Find |
|---|---|
| Angle A = 40°, Angle B = 70°, Side a = 10 | Side b and Side c |
b and c are lengths of side which can be calculated using the Law of Sines because angles are known.
When to Use the Law of Cosines
When having different types of info, it is when you apply the law of cosines. In most cases, it is useful in:
- Side-Angle-Side (SAS): When you know two sides and the included angle, you can easily find the third side.
- Side-Side-Side (SSS): When you know all three sides, the Law of Cosines helps you determine the angles of the triangle.
This is the way it operates, in case there is an instance where you possess:
| Given | Find |
|---|---|
| Side a = 6, Side b = 8, Angle C = 60° | Side c |
The length of side c can be computed cheaply by applying the Law of Cosines. When dealing with non-right triangles, this law becomes very important.
Real World Applications of Sines and Cosines
Numerous fields rely on the Law of Sines and the Law of Cosines for various real life uses. Some notable instances include:
- Engineering: Engineers often use these laws to design structures and analyze forces in triangles.
- Architecture: Architects apply these principles to ensure buildings are stable and visually appealing.
- Navigation: Pilots and sailors rely on these laws for accurate course plotting and distance calculations.
- Surveying: Land surveyors use the Law of Sines and Cosines to measure land areas and plot maps accurately.
You might discover these statutes to be of great utility in day-to-day undertakings such as:
- Determining the height of a tree by measuring angles from a distance.
- Calculating distances in hiking or outdoor navigation.
The grasp of such laws is instrumental not just in the academic world but also boosts your skills to solve problems in real life. It does not matter if you are measuring angles or calculating distances, the Law of Sines and the Law of Cosines are two very useful tools.
Common Mistakes in Using Sines and Cosines
While tackling the Sine Theorem and Cosine Theorem, it becomes simple to errect a few normal errors. Here are some misfortunes you should avoid:
- Incorrectly identifying triangle types: Make sure to determine whether you’re working with a right triangle, acute triangle, or obtuse triangle. Each requires different approaches.
- Not using the correct formula: Double-check which law to use. Remember, the Law of Sines is ideal for AAS, ASA, or SSA situations, while the Law of Cosines is for SAS and SSS scenarios.
- Forgetting to check for ambiguous cases: When using SSA, you might encounter two possible triangles. Always evaluate if both triangles can exist.
- Calculation errors: Simple arithmetic mistakes can lead to incorrect answers. Always recheck your calculations, especially when squaring numbers or taking square roots.
- Rounding too early: It’s best to keep full precision in your calculations until the final answer. Rounding too soon can lead to significant errors.
Awareness of these frequent errors will enhance your precision in solving problems on the Laws of Sines and Cosines. Always take your time and ensure that you are right!
Frequently Asked Questions
We will discuss a few frequently asked questions regarding the Law of Sines and the Law of Cosines:
- What is the difference between the Law of Sines and the Law of Cosines? The Law of Sines is used for finding missing angles or sides when you know two angles and one side or two sides and a non-included angle. The Law of Cosines is applied when you know two sides and the included angle or all three sides.
- Can I use these laws for right triangles? Yes, you can use both laws for right triangles, but the Pythagorean theorem is usually simpler.
- How do I know which law to use? Assess the information you have. Use the Law of Sines for AAS, ASA, or SSA cases, and the Law of Cosines for SAS or SSS cases.
- What if I only have angles? If you only know angles, you can find the sides using the Law of Sines once you have at least one side length.
These questions come in handy for resolving some misapprehensions plus they can also help you troubleshoot triangle-related issues.
Conclusion
It is very important for solving triangles to understand the Law of Sines and the Law of Cosines. Enhancing your problem-solving skills can be achieved by using them as often as possible, knowing when to use each law, avoiding common mistakes, and applying these principles on real life situations. Whether you are an engineer, architect or just someone who enjoys mathematics, remember that these laws are good weapons in your arsenal.
Keep on practicing, and feel free to refer back to this guide whenever you feel uncertain about using these laws. In time and with practice, you will gain more confidence in the application of the Law of Sines as well as the Law of Cosines in different scenarios. Have fun working on problems!